因為公開試將臨的關係最近也沒空寫新的文章了。綜觀過去一年似乎這網誌已完全轉型為數學/筆記的文庫了 XD 當然這個暑假還會陸續有來。
Physics
- 我打算將Atomic world跟compulsory part的nuclear energy合併成為同一份筆記,反正有很多重複的地方,另外我希望可以完成電磁學的筆記.
Chemistry
- 反應動力學(compulsory rate of reaction和elective Rate equation)可以合併
- 平衡反應
- 周期性及d-block元素
- 工業化學
我一直希望弄一些幾何性的文章但沒這種能力,也許我會寫一篇關於坐標幾何vs複平面的應用文章……另外我也沒空寫文了,希望考HKDSE以前可以完成Osu!的同人文。
Thursday, 28 July 2011
Tuesday, 19 July 2011
Interpretation on definition of inequalities
Recently I've read the pure mathematics textbook about inequalities, and here I want to discuss the definition about it, it's a philosophic issue more than some kind of mathematical calculation.
How to define inequality?
This is two definition from the book:
1) If x>y, then x-y > 0.
2) If x>y, then x/y > 1.
For me, these definition is not good enough as the nature of inequality wasn't shown.
Back to the numberline with integers, the element forming the integer set is based on a order of magnitude of numbers. Without order, numbers aren't showing their magnitude lost their meaning. On a number line, numbers are arranged in order and from small to big. The problem comes: the integer set contains infinitely many integers, so how do we arrange them in order? Wihtout any axioms we don't know their magnitude, so a base point is set, zero.
Zero is the symmetrical point and the ordering is based on the difference of the point from the zero. Another problem come as one number X are on the left of zero and another number Y is on the right of zero, |OX|=|OY| (lengths are directly comparable before it is quantitzed, they don't need the ordering of numbers), but since they are different points so they are unequal, how to distinguish X and Y? Then there's the need to invent the term "difference".
Difference implies unequal, then the unequal sign works in two way. If x>y, then y is smaller than x, otherwise x > y > x cause the contradiction of self unequal to self. By symmetrical means we will need two signs to interpret these relation.
Positive and negative.
When one is "more positive than" another, the "anthoer" is "more negative" to the original numbers. (These aren't limited to +ve vs +ve numbers because we consider the whole line).
Back to our main concern, x > y.
x is more positive than y.
What's the difference? x-y, the "more positive part".
Therefore "x-y" is positive.
That's the basic definition of inequalities rather than saying it "x-y > 0".
The difference "x-y" let it to be a.
Then x-y = a, x = a + y. y need to be "a more positive" to reach x.
On the numberline, OY + OA = OY + YA = OX, then y + a = x.
Now we can explain x/y > 1 since
"x can be divided into more than 1 portion of y, so x = y + a."
x/y = (y+a)/y = 1 + y/a > 1.
So we observe inequality by difference, not by dividing, this is the fundamental concept of inequalities. Of course in proving inequalites we don't need to be such strict because the properties are widely available from the basic definition already.
For the unequal sign, we know there's a difference but we don't know which why the inequality it is.
for x unequal to y,
case 1: x>y, then x = a + y, where a is positive
case 2: x < y, then x + a = y, or we say x = y + b, where b is negative.
combining gives "x unequal to y" is equivalent to "x = y + a" where a is non-zero. (+ve or -ve).
They looks easy, but worth thinking, that's what I've learnt.
e.g. Show the triangular inequality in terms of difference.
Consider triangle ABC, we are going to show AB+BC > CA.
In geometrical visualization we copy segment AB and BC on CA, and if it overlaps the inequlity is valid.
Step 1: draw a circle, center A and radius AB, intersect AC on D.
Step 2: draw a circle, center C and radius BC, intersect AC on E.
There'll be two intersection point, B and another point B'. It's easy to show that triangle ABC is congruent to triangle AB'C.
Now we consider the following logic:
1) two circle not sharing common tangents gives two intersection points.
2) the area enclosed by two intersection point is overlapped.
Since B' must be out of triangle ABC (otherwise it mustn't congruent to each other), therefore AD and BE overlapped, i.e. |DE| > 0. Proof complete.
Exercise:
1) Show that a^2 is non-negaitve in terms of difference.
2) Show that AM-GM inequality in terms of difference.
How to define inequality?
This is two definition from the book:
1) If x>y, then x-y > 0.
2) If x>y, then x/y > 1.
For me, these definition is not good enough as the nature of inequality wasn't shown.
Back to the numberline with integers, the element forming the integer set is based on a order of magnitude of numbers. Without order, numbers aren't showing their magnitude lost their meaning. On a number line, numbers are arranged in order and from small to big. The problem comes: the integer set contains infinitely many integers, so how do we arrange them in order? Wihtout any axioms we don't know their magnitude, so a base point is set, zero.
Zero is the symmetrical point and the ordering is based on the difference of the point from the zero. Another problem come as one number X are on the left of zero and another number Y is on the right of zero, |OX|=|OY| (lengths are directly comparable before it is quantitzed, they don't need the ordering of numbers), but since they are different points so they are unequal, how to distinguish X and Y? Then there's the need to invent the term "difference".
Difference implies unequal, then the unequal sign works in two way. If x>y, then y is smaller than x, otherwise x > y > x cause the contradiction of self unequal to self. By symmetrical means we will need two signs to interpret these relation.
Positive and negative.
When one is "more positive than" another, the "anthoer" is "more negative" to the original numbers. (These aren't limited to +ve vs +ve numbers because we consider the whole line).
Back to our main concern, x > y.
x is more positive than y.
What's the difference? x-y, the "more positive part".
Therefore "x-y" is positive.
That's the basic definition of inequalities rather than saying it "x-y > 0".
The difference "x-y" let it to be a.
Then x-y = a, x = a + y. y need to be "a more positive" to reach x.
On the numberline, OY + OA = OY + YA = OX, then y + a = x.
Now we can explain x/y > 1 since
"x can be divided into more than 1 portion of y, so x = y + a."
x/y = (y+a)/y = 1 + y/a > 1.
So we observe inequality by difference, not by dividing, this is the fundamental concept of inequalities. Of course in proving inequalites we don't need to be such strict because the properties are widely available from the basic definition already.
For the unequal sign, we know there's a difference but we don't know which why the inequality it is.
for x unequal to y,
case 1: x>y, then x = a + y, where a is positive
case 2: x < y, then x + a = y, or we say x = y + b, where b is negative.
combining gives "x unequal to y" is equivalent to "x = y + a" where a is non-zero. (+ve or -ve).
They looks easy, but worth thinking, that's what I've learnt.
e.g. Show the triangular inequality in terms of difference.
Consider triangle ABC, we are going to show AB+BC > CA.
In geometrical visualization we copy segment AB and BC on CA, and if it overlaps the inequlity is valid.
Step 1: draw a circle, center A and radius AB, intersect AC on D.
Step 2: draw a circle, center C and radius BC, intersect AC on E.
There'll be two intersection point, B and another point B'. It's easy to show that triangle ABC is congruent to triangle AB'C.
Now we consider the following logic:
1) two circle not sharing common tangents gives two intersection points.
2) the area enclosed by two intersection point is overlapped.
Since B' must be out of triangle ABC (otherwise it mustn't congruent to each other), therefore AD and BE overlapped, i.e. |DE| > 0. Proof complete.
Exercise:
1) Show that a^2 is non-negaitve in terms of difference.
2) Show that AM-GM inequality in terms of difference.
Friday, 15 July 2011
Irrationality
Rational and irrational numbers are an interesting topic and yet not all the problems in the related field has been solved fully. I shall now introduce some basic properties of it.
1) Group as an algebraic structure have the following properties
For a group G there exist a function, say * here.
(Just recall that the function maps a single element from a set to a unique element in co-domain.)
-Closure. i.e., if , then
, then 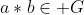 .
.
-Associativity:
-Existance of identity: exist identity such that
identity such that  , it's often written as 1 (Since 1 is the identity of real/rational # under multiplication.)
, it's often written as 1 (Since 1 is the identity of real/rational # under multiplication.)
-Existance of inverse element: for every , exist
, exist  (it can be a) such that
(it can be a) such that  . (However there are theorem saying that if ab = e, then ba = e). We say
. (However there are theorem saying that if ab = e, then ba = e). We say  . (NEVER a = 1/b)
. (NEVER a = 1/b)
Example: non-zero Rational number with multiplication is a group, identity 1.
2) Rational numbers can be written in forms of p/q where p is integer and q is natrual number. More precisely rational numbers have their own unique expressions if (|p|,|q|) = 1.
Inversely irrational numbers can't be expressed in fractions, this gives us the fundamental way to show that a number is irrational.
Example 2: Prove is irrational.
is irrational.
Classic question. Assume .
.
By squaring both sides and change of term, we have .
.
Then following logic finishes the prove by contradiction.
 .
.
Now we will introduce another method to show irrationality.
Assume are two simpliest distinct rationals with
are two simpliest distinct rationals with 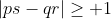 , then
, then  so that we can write a real number in a series of fractions. More importantly, irrational numbers can't be written in finite numbers of fractions.
so that we can write a real number in a series of fractions. More importantly, irrational numbers can't be written in finite numbers of fractions.
Corollary: Fractions, in decimal, are recurring.
Prove: Consider prime p, we are going to prove 1/p is recurring.
Consider Fermat's little theorem, .
.
Therefore p is a divisor of .
.

Therefore 1/p is recurring.
Note that recurring period may not be p-1 if it can be further simplified, but the general trend is rising.
Proof: For every , there exist finite prime factors so that they are generally used up, so that larger primes are GENERALLY mapped to higher n.
, there exist finite prime factors so that they are generally used up, so that larger primes are GENERALLY mapped to higher n.
Then if the recurring decimal is infinity, it is irrational. That gives the idea to prove a number being irrational.
Example 3: Prove e is irrational.
Consider , set
, set  , it's a fraction with denominator n!.
, it's a fraction with denominator n!.
 , it follows that we can't express e in finite number of fractions, so we have completed the proof.
, it follows that we can't express e in finite number of fractions, so we have completed the proof.
Another approach is directly combining terms by definition, since the expressed forms in simpliest terms* monotonically increase, the sum has a infinitely large denominator, hence irrational.
4) Back to out main concern, we would like to show some properties of irrational numbers.
- Irrational numbers do not perform closure under most elementary functions.
Example 4: Proof the existance of infinite pairs of (x,y) where x,y are irrational and x+y, xy are rational. More precisely, show that for every irrational x show that there's infinitely many y satisfying the condition.
Proof: Let where r is rational.
where r is rational.
 , with root
, with root  by adjusting r obviously there exist many r such that the outcoming x is irrational. Our prove is then completed.
by adjusting r obviously there exist many r such that the outcoming x is irrational. Our prove is then completed.
5) Show that is irrational.
is irrational.
This is a bit tricky. We show it by De Morive's theorem.
By expanding , we find that cos nx are expressed in terms of P(cos x), where P is a polynomial of rational coefficients. Therefore irrationality of cos nx implies irrationality of cos x. Consider the irrationality of
, we find that cos nx are expressed in terms of P(cos x), where P is a polynomial of rational coefficients. Therefore irrationality of cos nx implies irrationality of cos x. Consider the irrationality of  , the proof is completed.
, the proof is completed.
Exercise:
1) Show that (Z,+) is a group.
2) Show that is irrational.
is irrational.
3) Show that is irrational by showing that it can't be written in finite fractional.
is irrational by showing that it can't be written in finite fractional.
4) Show that irrational numbers can be written in continued fraction of infinite length.
5) Show that 37 is a factor of 999 considering 1/37.
6) Provide a full mechanism such that there's infinite r to satisfy the considition "x,y, irrational and x+y, xy rational".
7) Discuss the countability of irrational numbers.
8) Discuss the countability of irrational pairs (x,y) such that x+y and xy are rational.
9) If x,y are irrational while is rational. Find all possible x+y with proof.
is rational. Find all possible x+y with proof.
10) Show that is irrational.
is irrational.
11) For , if y is rational, prove the primitive root of x (
, if y is rational, prove the primitive root of x ( ) is irrational, unless it is trivially rational (e.g. tan 0 = 0).
) is irrational, unless it is trivially rational (e.g. tan 0 = 0).
12) Show that is irrational.
is irrational.
13) If x,y are rational numbers with x>y, show that there exist rational numbers a,b and irrational number c that x>a>c>b>y. Hence prove real number is dense.
Extra infomation: we prove the transcendency of a number by similar method but stricter bounding. You can visit the page talking about Liouville's numbers. Then finish this question:
CGMO 2007 day 2 Q3
If a,b,c are integers that and define
and define  satisfying
satisfying  is smaller than 0.0001, prove that
is smaller than 0.0001, prove that  .
.
1) Group as an algebraic structure have the following properties
For a group G there exist a function, say * here.
(Just recall that the function maps a single element from a set to a unique element in co-domain.)
-Closure. i.e., if
-Associativity:
-Existance of identity: exist
-Existance of inverse element: for every
Example: non-zero Rational number with multiplication is a group, identity 1.
2) Rational numbers can be written in forms of p/q where p is integer and q is natrual number. More precisely rational numbers have their own unique expressions if (|p|,|q|) = 1.
Inversely irrational numbers can't be expressed in fractions, this gives us the fundamental way to show that a number is irrational.
Example 2: Prove
Classic question. Assume
By squaring both sides and change of term, we have
Then following logic finishes the prove by contradiction.
Now we will introduce another method to show irrationality.
Assume
Corollary: Fractions, in decimal, are recurring.
Prove: Consider prime p, we are going to prove 1/p is recurring.
Consider Fermat's little theorem,
Therefore p is a divisor of
Therefore 1/p is recurring.
Note that recurring period may not be p-1 if it can be further simplified, but the general trend is rising.
Proof: For every
Then if the recurring decimal is infinity, it is irrational. That gives the idea to prove a number being irrational.
Example 3: Prove e is irrational.
Consider
Another approach is directly combining terms by definition, since the expressed forms in simpliest terms* monotonically increase, the sum has a infinitely large denominator, hence irrational.
4) Back to out main concern, we would like to show some properties of irrational numbers.
- Irrational numbers do not perform closure under most elementary functions.
Example 4: Proof the existance of infinite pairs of (x,y) where x,y are irrational and x+y, xy are rational. More precisely, show that for every irrational x show that there's infinitely many y satisfying the condition.
Proof: Let
5) Show that
This is a bit tricky. We show it by De Morive's theorem.
By expanding
Exercise:
1) Show that (Z,+) is a group.
2) Show that
3) Show that
4) Show that irrational numbers can be written in continued fraction of infinite length.
5) Show that 37 is a factor of 999 considering 1/37.
6) Provide a full mechanism such that there's infinite r to satisfy the considition "x,y, irrational and x+y, xy rational".
7) Discuss the countability of irrational numbers.
8) Discuss the countability of irrational pairs (x,y) such that x+y and xy are rational.
9) If x,y are irrational while
10) Show that
11) For
12) Show that
13) If x,y are rational numbers with x>y, show that there exist rational numbers a,b and irrational number c that x>a>c>b>y. Hence prove real number is dense.
Extra infomation: we prove the transcendency of a number by similar method but stricter bounding. You can visit the page talking about Liouville's numbers. Then finish this question:
CGMO 2007 day 2 Q3
If a,b,c are integers that
Thursday, 7 July 2011
Problem on divisibility and GCD
There are quite a lot of methods to proof a number involved in a equation as a perfect square, we will finish this one by the factorization method introduced last time.
Assume
$x=k_{x}k_{xy}k_{xz}k_{xyz}$
$y=k_{y}k_{xy}k_{yz}k_{xyz}$
$z=k_{z}k_{xz}k_{yz}k_{xyz}$
Recall that $(k_{x},k_{y},k_{z})=(k_{xy},k_{xz},k_{yz})=1$
Since $(x,y,z)=1$, $k_{xyz}=1$.
Consider $x+y=\frac{xy}{z}=\frac{k_{x}k_{y}}{k_{z}}(k_{xy})^2$, what we are going to proof is that $\frac{k_{x}k_{y}}{k_{z}}=n^2$, but of course it's good if it is 1, so we will proof that $k_{x}=k_{y}=k_{z}=1$ by showing that $\prod k_{xy}$ is equal to x,y or z.
When $\frac{xy}{z}$ is an integer, we say all factors of z has been used up by x and y, then $k_{xz}k_{yz}=z$, then obviously $k_{z}=1$. Similarly (Q1) we can show similar case for x and y. Then $x+y=k_{xy}^2$ and the proof is done. The proof for (x-z) and (y-z) is left for readers.
A famous solution on IMO 1988 Q6, where a,b are positive integers and $\frac{a^2+b^2}{ab+1}=k$is a integer, then it's a perfect square. The following infinite descent method is done by a contestant who won a special prize that year.
Assume k is not perfect square, then k>2. Since the expression is symmetrical we WLOG assume $x\geq y$, but for x=y, k<2 and the assumption can't stand, therefore a > b.
Consider the minimal pair of a+b. Consider the following equation $x^2-kbx+b^2-k=0$, by the given information a is one of the root. Let a' be another root. By Viete's theorem, $a+a'=kb$, $aa'=b^2-k$, then a' is an integer. Note that a' is also a set of solution that $\frac{a^2+b^2}{ab+1}=k$.
By $k(1+a'b)=a'^2+b^2>0$, b>1, then we have a'>0.
Also, $a'=\frac{b^2-k}{a}<\frac{b^2}{a}<a$, a'+b is smaller than a+b, contradicts the assmption that a+b is the minimal solution. Then k must a perfect square.
Q1 Refer to the bolded line, proof that $k_{x}=k_{y}=1$.
Q2 We have only proofed x+y is a perfect square only so far. Finish the proof by using similar idea with Q1.
Q3 Find number of pairs of natrual number where a-b is a prime and ab is perfect square.
Q4 a,b,c are natrual numbers, a=20, b|c, find all triples (a,b,c) that a,b,c are in harmonic progression.
Q5 Find all natural number triples (a,b,c) that [a,b,c]=a+b+c.
Q6 Show for all integer n>11, $n^2-19n+89$ is not a perfect square.
Q7 Find all positive interger n such that $n^2+89n+2010$ is a perfect square.
Extra question:
The proof on IMO 1988 Q6 is based on the contradictory point between (1) a+b is minimal; (2) k is not a perfect square. [i.e. prove by contradictory since (1) => (2) => ~(1)]
Then, show that how the proof failed when k is a perfect square.
Sunday, 3 July 2011
Bridge plays
Recently I've played quite a number of boards of bridges on my android phone, while some are worthy to be shared.
1) Contract 5D (NS Vul)
Bidding
N E S W
1C / 1D 1S
2C / 2D /
5D a.p.
North
S J83
H ----
D AQJT
C AQJT87
South
S KT4
H A62
D K6543
C 54
West lead D5, how to play?
It would be easy if the distribution is even. However D was 3-1 break while S was 6-1 break, H 7-2 break. We will need a saftier way to make this contract.
In the first turn, we discard S 5 and win by H A. Play small hearts and ruff by D A to make sure that we have bridge to the declarer. Play 2 rounds of D, thrown in to W by C 10 to W's C K. West plays S A, then he'll have no choice but to play D or S, then back to declarer, cash D and let dummy get the remaining C.
What can we do if D is in 4-0 break?...
2) 1NT x + 3
North
S K854
H AJ4
D KT
C KJT6
South
S 76
H QT8765
D J3
C A74
N E S W
/
1N X a.p.
East leads S Q.
This contract can't be defeated. Playing small S and let E to play for the second round, East plays D A and S A, D 7 to D K.
Since East doubled, C Q is probably on E, and we hope that H K is on W. The is correct, and we finally wins 4C and 6 H.
What we want to know is that whether we can play a game. But it may be quite risky as the position of K and As may be bad. However if E leads, they won't have the chance to win the D tricks...
1) Contract 5D (NS Vul)
Bidding
N E S W
1C / 1D 1S
2C / 2D /
5D a.p.
North
S J83
H ----
D AQJT
C AQJT87
South
S KT4
H A62
D K6543
C 54
West lead D5, how to play?
It would be easy if the distribution is even. However D was 3-1 break while S was 6-1 break, H 7-2 break. We will need a saftier way to make this contract.
In the first turn, we discard S 5 and win by H A. Play small hearts and ruff by D A to make sure that we have bridge to the declarer. Play 2 rounds of D, thrown in to W by C 10 to W's C K. West plays S A, then he'll have no choice but to play D or S, then back to declarer, cash D and let dummy get the remaining C.
What can we do if D is in 4-0 break?...
2) 1NT x + 3
North
S K854
H AJ4
D KT
C KJT6
South
S 76
H QT8765
D J3
C A74
N E S W
/
1N X a.p.
East leads S Q.
This contract can't be defeated. Playing small S and let E to play for the second round, East plays D A and S A, D 7 to D K.
Since East doubled, C Q is probably on E, and we hope that H K is on W. The is correct, and we finally wins 4C and 6 H.
What we want to know is that whether we can play a game. But it may be quite risky as the position of K and As may be bad. However if E leads, they won't have the chance to win the D tricks...
Subscribe to:
Posts (Atom)
