This one requires some very basic college knowledge but is probably neglected by most students. With such deriving approach we can remember much less identities and realize more of the beauty of mathematics.
Part I - Nature of exponential function
In college level we first define the number e and the textbook will probably show that expansion of e directly, in better case we can get that expansion series with Taylor expansion, but that's not rigour enough. A more advanced and appropiate way is to show the expansion series of e itself, is exponential.
Definition.

is defined as the exponential function. Note that z is used instead of x because we want complex number involving here.
Lemma.

Since we are not assuming

as exponential, we shall demonstrates its properties. Note that

is trivial in the expansion series, we have

by product rule, i.e.,

is constant, and when z=0 the constant is exp(c). Now set z=a, c=a+b gives the expected result.
There could be more properties to be shown, but that's enough for us to state it as exponential.
Bridge between exponential function and trigonometric functions
Definition.

and

.
Now

, so

Substitute them into the expansion series gives

and

.
And again, it automatically fits the Euler Identity:

,

, and

. Following with the angle sum identites, showing that the function defined is the trigonometric function. (Note: the function equation concerning angle sum formula has unique solution of trigonometric function as above, this is beyond our discussion.
Part II - deriving trigonometric identities
This part is already included in my BAS note, but I'd want to show this one again.
Theorem.

Proof: Equating the expansion of


Equating real and imaginary part,

.
Theorem.

Proof.


There're another trick dealing with trigonometric functions at higher power.
Example. Evaluate

In most textbook we will try to use reduction formula, or transform it into forms of

but we can also change it into trigoonometric function of degree 1 to deal with it.
Let

, then

. Similarly,

,

.
Observe that

and

Now



By such a transformation the integration could be done easily. Note that

.
Part III - transformation of complex number into polar (cis) form
Definition. Polar form of complex number is in form of

where

The second part of the statement is called De Moivre's theorem.
The proof is simple considering the multiplication in forms of

, and by angle sum formula.
Example. Turn

into polar form.
Solution.

Example. Turn

into polar form.
Solution.



.
Part IV - analogy on real polynomial identities
Example. Show that

.
In fact this is a lemma from the theorem that "any prime can be resolved into sum of two perfect squares."
It can be done by direct expansion, but we can make it by complex number:
Let

,
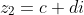

, done.
Example. Show that

Note that

(n=0,1,2,3, n=0 -> 1 roots) are the roots of

, summing the roots gives

(the imaginary parts eliminates each other since

), so we get the desired result.
More to explore:
I) Expand tangent and cotangent in terms of polynomials.
II) Express

and

by trigonometric functions of the first degree with proof by complex numbers.
III) Turn

into polar form, and show that

IV1) Evaluate

IV2) In fact we have another real identities concerning sum of four squares:

which can be proved by
quaternion numbers. Search for quaternion numbers and prove the above identity by quaternion numbers.
Reference
Walter Rudin. Real and complex analysis. (In fact, the analysis on exponential series is commonly appearing in most books)
Margaret M.Gow. A Course in pure mathematics.
