Edit: well I don't recommend people playing the original Wordle, which is now under NYT due to their hideous changes to the game, including banning words from dictionary, making answer words notoriously difficult, and ADDING AD TRACKERS ON THE GAME SITE.
Although we won't possibly try Wordle anymore...the science behind the game is still fun to look into. There are also other interesting non-commercial variants like those I listed below. I hope you will spend a little time trying and feel fun about those :)
Recently it has became a trend to play Wordle or its variant: Nerdle, Kotobade Asobou, Primel,... and you can extend the list for another 10 or more games.
From a computational perspective, finding the optimal route is easy given the fixed dictionary set and the limited word length (5). Not necessarily the best but the entropy approach is classic (cf. strategies against games like hangman), efficient and near optimal. 3Blue1Brown made two very high quality videos (as usual) which you can find here and there.
The only thing to point out is that the overall efficiency (distribution on number of guesses) relies on how you weight the frequency/likelihood of those answer-words. It is fine not to assume anything (word frequency), but if any I would set the cut-off (the inflexion point for the sigmoid function) much much narrower given that most answer-words seems to be common enough, more common than the impression from the actual pool size (~2300 words). Of course the ideal weighting is to equate the frequency of occurrence for words as answer, but that would be a meta thing to consider after.
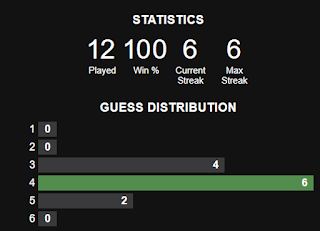
I have been using the same starter from day 1 -- POWER. Clearly not the most efficient as O and E are not the most popular vowels and W is fairly uncommon, but I feel like to stick with that and see how do I perform. So far so good: I averaged 3.6 guesses over the past games.
But English is never my specialty...it would be more interesting to talk about Nerdle, the one based on numbers and the four arithmetic operators. Mahjong Handle is also fun given its totally different nature and an essentially harder variant to tackle.
Nerdle.
10 numbers, 4 operators and the equal sign, with 8 slots and 6 guesses. A much easier game given its highly predictable pattern (math based) and a small letter pool size. In fact there are two starters that covers all 15 letters that you can almost always guess it right on the third guess with some exception.
The first exception comes from equivalence by operator inverses. For example 12/3 = 4 can be expressed as 4*3 = 12. Such equivalence can usually be eliminated once you know which operator appears and which does not.
The second exception comes from equivalence upon translation for + and -. For example 3+8=11 translates to 5+8=13. Again it can be eliminated by fully exhausting all 10 possible numbers with proper starters. (It is in fact possible for translation to happen using the same set of numbers. Can you find one? -- just keep reading if you can't :P)
The third exception is by commutativity. For example 6+9=15 swaps to 9+6=15, 12/3=4 swaps to 12/4=3 and so on. Unlike the previous two exceptions, the starters do not necessarily eliminate commutativity. In fact, the author of Nerdle said that it won't be fun without allowing commutativity...although he added the choice of playing the game that accepts equivalent commutated answer at the end.
The strategy is simple from here: you use the two starters (in a very rare case if the first starter is good enough one may also give it a try). Once you know all the symbols appearing in the expression it should be easy to get the right answer in the third guess (upon commutativity). There many ways for one to eliminate most random permutations of letters:
- RHS is presumably a single number without operators. The equal sign should appear on the 5th-7th slot, which is then clear from the starters. That means the expression on the left consists of 4-6 letters with 1 or at most 2 operators. You can then guess the position of those operators before filling the numbers in.
- The possibility for RHS is greatly limited by the operators given. An expression with single digit numbers, + and - only would not exceed 19/29 and you know the 1 must be at the 6th slot (if ='s on the 5th). Checks like mod 10 are also very helpful.
Take Nerdle#20 as an example. The two starters told you that the letters are 1, 3, 5, 6, + and =; also = is at 6th with +, 1, 6, 5 not at 2nd, 3rd, 7th and 8th slot respectively. What's the correct answer?
With 5 slots on LHS and only + allowed the answer is either a sum of 3 single digit numbers or a sum of two double digits. Let's look at the possibility of a sum of three single digit numbers. Clearly RHS must be 1x: 11 and 13 are too small as 6+5+3=14; 15 is not allowed and the only combination that sums to 16 is 6+5+5 where 3 is missing.
What about a sum of two double digits? By checking mod 10 the possibilities for the ones are 1+5=3+3=6, 5+6=11 and nothing else. Notice that the tens on RHS is not 6 but it's not 11 either, so we need an extra 10 from the ones meaning that the ones must be 5 and 6. We now look for combinations that add to 2, 4 or 5 (so that the corresponding tens would be 3, 5 or 6). The possibilities are 1+1=2 and 1+3=4.
Plugging in we conclude that we have two distinct expressions satisfying the hints from the two starters: 15+16=31 and 15+36=51. One of them would be the third guess and if that fails we know for sure what's the right answer at the fourth guess even without commutativity (why?).
*
The phenomenon of "when your first serious attempt (for the right answer) failed you can easily give the correct answer right away" is important because not only that the chance of getting right is respectable, but it is also informative for you to get the right answer even if it doesn't work. In that way we have largely avoided the long tail cases (guessing 5+ times) and compresses the average number of guesses required to the minimum. But what about games where long tail cases are well possible?
Welcome to the world of Mahjong Handle, where you guess a given valid hand in 6 guesses.
*I never play Mahjong in English and I guess that applies to most of you guys...check Wiki if you are not sure about the terminology.
How hard is Mahjong Handle? We start by counting the number of valid winning hands in Japanese mahjong. I am sure there is a calculated number somewhere on the web, but to make it simpler we consider a very restricted yaku type -- all triplet hand (対々和) where you need 4 triplets and a pair. Simple math tells you that there are C(36,4)*32 = 1884960 ways to score an all triplet hand and that is already 1000 times as massive as Wordle's answer pool! There is no doubt that the actual number of valid hands is at least 20 times larger...or 50 times, 100 times maybe?
With that in mind, exhaustive information theory approach isn't practical anymore (another differences between Wordle and Mahjong Handle is that frequency analysis doesn't work here -- at least there is no obvious frequency references). Even if one managed to estimate the information provided by each guesses one must face the long tail problem. Unlike Nerdle, it may take up to 2 extra necessary guesses. Given the overall complexity of the game it often decides whether one gets it within 6 guesses or not.
To give a more solid example one may consider the combination 2223334 and you are waiting for one extra tile. The extra tile can be 2, 3 or 4:
2: 222 234 33
3: 22 234 333
4: 222 333 44
While you may not know anything about whether it's 2, 3 or 4 in previous guesses. Things can be taken to extreme in the case of nine gates(九蓮宝燈) where all nine tiles are possible in the case of 11123456778999.
Gathering information on appearance is cheap, but information on repetition is expensive because it takes up multiple slots. It's even more expensive to ask if a tile appears 3 or 4 times, yet it's always possible given that triplet is a basic block in the hand.
As a consequence we often fall into a long tail trap where the remaining uncertainty is low, but each guess would only help by a little. The simple greedy approach as in the video (entropy + probability) may not work very well, but I bet that a secondary correction would help greatly (note: 3Blue1Brown also mentioned this in his second video).
The real challenge is to evaluate each pieces of information gathered from the guesses though. Since exhaustive evaluation is now impossible, we can instead assign weightings to different kinds of partial information regarding the building block of 3 or 2. Rating from the least to the most useful information:
- a given tile is not in the hand
- a given tile is in a hand
- a tile is in a hand and is isolated from the sides
- a tile is in a given block
- a tile is in a block of sequences
- a sequence block with 2 known tiles
- a fully known sequence block
- a fully known triplet block
- a fully known block and isolated from the sides
...
Of course there are technical problems where blocks are often ambiguous when they stick together, but the idea should be clear: we assign weightings to each categories of information and play Mahjong handle prioritizing guesses according to the weightings assigned. We then adjust weightings to improve efficiency. No optimal performance guaranteed (as for any non-convex optimization), but it should be good enough.
And for humans like us how do we tackle the game?
Well I don't have any concrete suggestions even for starters. Thirteen orphans(国士無双) is certainly something to start with, but some says that these terminal tiles do not actually appear in hands *that* often comparing to the simple 13/36 coverage. Some also suggests the use of seven pairs due to its flexibility and to detect repetition but some also say that to be a waste. Some prefer to use loads of sequences...it's hard to tell which one's the best but I ended up using thirteen orphans as my starter. There are two reasons for that:
1) Coverage is still important. It is still very probable for at least one of the 13 tiles to appear in the hand and this is the cheapest way to ask for all 13 of them in one go.
2) Detecting honor tiles are very costly. In normal hands you need 2 or 3 copies of an honor tile for the hand to be valid, but for thirteen orphans you only need a single copy of it. This is another long tail problem -- any of the seven honor tiles may appear in your hand. Any algorithm that neglects them will face the chance of wasting 2 or 3 extra guesses at the end just to detect them.
After that it's also about detecting sequences and repetitions. When both terminals (1,9) are void from the hand you can detect any sequence with 3 tiles (456), although repetition of 2, 3, 6 and 7 will be harder to detect. Some would prefer the use of two sequences (e.g. 234+678) to avoid that. Which is the better approach? I can't really tell.
For Wordle and Nerdle, one starts making reasonable attempt at guess number 3, but for Mahjong handle the guess should start no earlier than the fourth guess. From here you can really pile up something close to the answer and complete the final pieces using the ordering hints. There are too many 'rules' to apply and I can't even count them all, but here is one for example: if you have two consecutive tiles (e.g 56s) one labelled orange and one labelled blue then these two tiles must be a repetition of the tile labelled blue (why?).
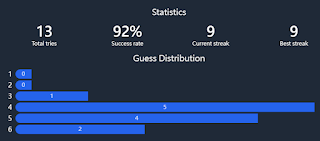
Still getting it right on the fifth guess is not that easy and here is my stats:
There are definitely better strats as observed from the daily performance of my friends, but I enjoyed more the later guesses for this game and haven't bothered to optimize the overall approach (yet). If you have any ideas please comment and tell me that :D